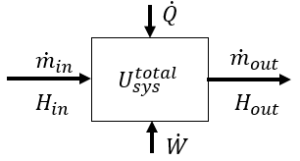
Energy balance (ignoring kinetic and potential energies):

\[\frac{dU_{sys} ^{total}}{dt} = \dot{m}_{in} H_{in} – \dot{m}_{out} H_{out} + \dot{Q} + \dot{W}\]

where \(U_{sys} ^{total}\) is the total internal energy of the system at anytime (kJ)
\(H_{in}\) and \(H_{out}\) are specific enthalpies (kJ/kg)
\(\dot{m}\) is a mass flow rate (kg/s)
\(\dot{Q}\) is heat added per time (kJ/s)
\(\dot{W}\) is work added per time (kJ/s) and it includes both shaft work and expansion/compression work.

For a system with no outlet stream and an inlet stream of constant enthalpy, the integrated for of the first law is:

\[m_f U_f – m_i U_i = (m_f – m_i)H_{in} + Q^t + W^t\]

where \(m_i\) is the mass in the system at \(t = 0\)
\(m_f\) is the mass in the system at time \(t\)
\(U_i\) is the specific internal energy (kJ/kg) in the system at \(t=0\)
\(U_f\) is the specific internal energy (kJ/kg) in the system at time \(t\)
\(H_{in}\) is the specific enthalpy (kJ/kg) of the feed stream
\(Q^t\) is the heat added in time \(t\) (kJ)
\(W^t\) is the work added in time \(t\) (kJ)
Therefore \(m_f – m_i\) is the total mass added to the system.

Steady-state adiabatic compressor or turbine: \[\dot{m}_{in} H_{in} + \dot{W}_S = \dot{m}_{out} H_{out}\] where \(\dot{W}_S\) is the shaft work per time

Throttle:   \[H_{in} = H_{out}\]

Adiabatic reversible expansion or compression (open or closed system) for an ideal gas:

\[\frac{T_2}{T_1} = \left( \frac{P_2}{P_1} \right) ^\frac{R}{C_P}\]