Material Balances: Screencasts
A general material balance is presented and simplifications of the balance are shown for different processes.
We suggest you list the important points in this screencast as a way to increase retention.
Reviews material balances using a flash system.
We suggest you list the important points in this screencast as a way to increase retention.
Important Equations:
Overall steady-state material balance:
\[ \stackrel{.}{m}_{in} = \stackrel{.}{m}_{out} \]
where \( \stackrel{.}{m}_{in} \) is the total mass flow into the system per unit time, and \( \stackrel{.}{m}_{out} \) is the total mass flow out of the system per unit time. If a reaction is involved, the mass balance can be performed on individual atoms.
At steady state with no reaction, material balances are done on individual components. For example:
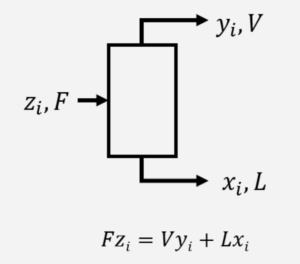
where \( F \), \( L \), and \( V \) are mass flow rates (kg/s) and \( z_{i} \), \( x_{i} \), and \( y_{i} \) are mass fractions of component \( i \) in each stream. A material balance can be done for each component.



