Gas-Phase Chemical Equilibrium: Screencasts
Explains why the equilibrium constant is dimensionless and why it is independent of pressure.
We suggest you list the important points in this screencast as a way to increase retention.
Derives the Van’t Hoff equation that shows how the equilibrium constant changes as temperature changes and simplifies for the case that the heat of reaction is constant.
We suggest you list the important points in this screencast as a way to increase retention.
Discusses the effect of adding an inert gas at constant temperature to a chemical reaction at equilibrium at either constant pressure or constant volume.
We suggest you list the important points in this screencast as a way to increase retention.
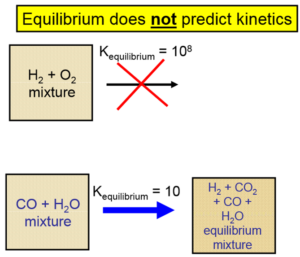
Important Equations:
Change in Gibbs free energy of a reaction at standard conditions:
\[\Delta G^{\circ} _T = \sum _i \nu _i \Delta G^{\circ} _{f,i}\]
where \(\Delta G^{\circ} _T\) = change in Gibbs free energy at standard conditions (ideal gas at 1 bar pressure for gases) at temperature \(T\),
\(\nu _i\) = stoichiometric coefficient for component \(i\)
\(\Delta G^{\circ} _{f,i}\) = Gibbs free energy of formation of component \(i\) at the same temperature \(T\).
\[exp \left( -\frac{\Delta G^{\circ} _T}{RT} \right) = K_a\]
where \(R\) = ideal gas constant,
\(T\) = absolute temperature
\(K_a\) = equilibrium constant, which is dimensionless.
The pure component fugacity at 1 bar for an ideal gas is 1 bar.
For ideal gases:
\[K_a = \prod _i (y_iP)^{\nu _i}\]
where \(y_i\) = gas-phase mole fraction.
\[\frac{\partial (\Delta G^{\circ} _T/RT)}{\partial T} = \frac{\partial (-lnK_a)}{\partial T} = -\frac{\Delta H^{\circ} _T}{RT^2}\]
where \(\Delta H^{\circ} _T\) = heat of reaction at standard conditions at temperature \(T\).
If the heat of reaction is assumed independent of temperature (a reasonable assumption for many reactions if the temperature range is not too large):
\[ln \left( \frac{K_2}{K_1} \right) = \frac{\Delta G^{\circ} _1}{RT_1} – \frac{\Delta G^{\circ} _2}{RT_2} = -\frac{\Delta H^{\circ} _{rxn}}{R} \left( \frac{1}{T_2} – \frac{1}{T_1} \right)\]
where \(K_1\) and \(K_2\) are equilibrium constants at absolute temperatures \(T_1\) and \(T_2\) respectively
\(\Delta H^{\circ} _{rxn}\) = heat of reaction, which is independent of temperature.
\[K_a = P\hat{a}^{\nu_i} _i\]
where \(\hat{a} _i = \hat{f}_i /f^{\circ} _i\) which is the thermodynamic activity,
\(\hat{f} _i\) = fugacity of component \(i\) in the mixture
\(f^{\circ} _i\) = fugacity of the pure component \(i\) at standard pressure (1 bar) and the temperature of the system.
