Gas-Phase Chemical Equilibrium: Interactive Simulations
These simulations were prepared using Mathematica. Download the free Wolfram player, and then download the simulation CDF file (link given below or click on figure to download). Try to predict the behavior when a parameter changes before using a slider to change that parameter. For these simulations, screencasts are provided to explain how to use them.
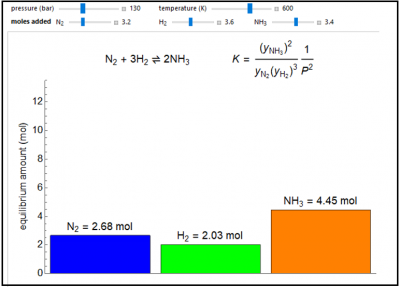
The number of moles at equilibrium is calculated for the Haber process, which is the reversible, exothermic reaction that synthesizes ammonia (NH3) from hydrogen (H2) and nitrogen (N2). The reaction is typically carried out at around 200 bar and 675–725 K. You can vary the pressure and temperature in this Demonstration. Gases are assumed to behave ideally, although realistically at the high pressures used in this reaction, there is significant deviation from ideal behavior. At equilibrium, you can add additional nitrogen, hydrogen, and/or ammonia at constant pressure, and the effect on the equilibrium is observed.
Try to answer these questions before determining the answer with the simulation. We suggest that you write down the reasons for your answers.
- As temperature increases, does the number of moles of NH3 increase or decrease?
- As pressure increases, does the number of moles of NH3 increase or decrease?
- Is it possible at low H2 concentrations to add N2 to the system and observe the reaction shifts to the left (i.e., less NH3 is present at equilibrium)?
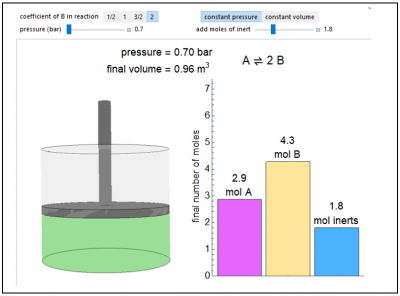
This Demonstration calculates the number of moles at equilibrium for a gas-phase reaction A ↔ rB, where A and B are ideal gases; the value of r (1/2, 1, 3/2, or 2) is selected with buttons. Initially the container is filled with 5 mol of reactant A, and equilibrium is obtained at either constant pressure (the pressure is set with a slider) or constant volume (the starting pressure is set with a slider). The bar graph displays the number of moles at equilibrium, including the moles of inert gas (the moles of inert are selected with a slider). The height of the piston is proportional to the final volume.
Try to answer these questions before determining the answer with the simulation. We suggest that you write down the reasons for your answers.
- For a reaction in which one mole of reactant makes two moles of product, will equilibrium conversion be higher for a constant-pressure or a constant-volume, isothermal reactor?
- If the reaction A↔2B is at equilibrium in a constant-pressure reactor and the pressure increases by adding more weight to the piston, which direction does the reaction shift to reach equilibrium?
- For a reaction in which two moles of reactant make one mole of product, will adding an inert increase or decrease equilibrium conversion in an isothermal constant-volume reactor? Assume ideal gases.
- For a reaction in which two moles of reactant make one mole of product, will adding an inert increase or decrease equilibrium conversion in an isothermal constant-pressure reactor? Assume ideal gases.