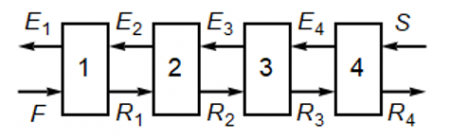
\[\dot F + \dot S = \dot M = \dot E_1 +\dot R_N\]

where \(\dot F\) is the feed flow rate (kg/h)
\(\dot S\) is the solvent flow rate (kg/h)
\(\dot M\) is the combined feed plus solvent flow rates (kg/h)
\(\dot E_1\) is the extract flow rate leaving stage 1
\(\dot R_N\) is the raffinate flow rate leaving the last stage (the Nth stage). See the above figure.

Mass balances for the case where the solvent contains no solute:

Solute A: \(x^F _A \dot F = x^M _A \dot M\)

Solvent S: \(x^F _S \dot F + \dot S = x^M _S \dot M\)

\[x^M _A + x^M _S +x^M _C = 1\]

where \(x^i _A, x^i _S\), and \(x^i _C\) are the mass fractions of solute, solvent, and carrier, respectively, in the flow stream \(i\) (\(\dot F, \dot S, \dot M\)).

The mixing point M is located on the ternary phase diagram using the lever rule:

\[\frac{\dot S}{\dot F} = \frac{\overline {MF}}{\overline {MS}}\]

where \(\overline {MF}\) is the line segment from the mixing point composition to the feed composition, and \(\overline {MS}\) is the line segment from the mixing point composition to the solvent composition.

The operating point \(P\) results from rearranging the overall mass balance (\(\dot F + \dot S = \dot M = \dot E_1 + \dot R_N\)) to yield:

\[\dot P = \dot S – \dot R_N = \dot E_1 – \dot F\]

This can be arranged to:

\[\dot P + \dot R_N = \dot S \,\,and \,\, \dot P + \dot F = \dot E_1\]