Single-Component Phase Equilibrium: Interactive Simulations
These simulations were prepared using Mathematica. Download the free Wolfram player, and then download the simulation CDF file (link given below or click on figure to download). Try to predict the behavior when a parameter changes before using a slider to change that parameter. Screencasts below explain how to use these simulations.
Simulation: Pressure-Temperature Phase Diagram for Water
Try to answer these questions before determining the answer with the simulation. We suggest that you write down the reasons for your answers.
- Which phase change requires the most heat to go from one phase to another isobarically?
- When undergoing a phase change isothermally, where is the biggest specific volume change?
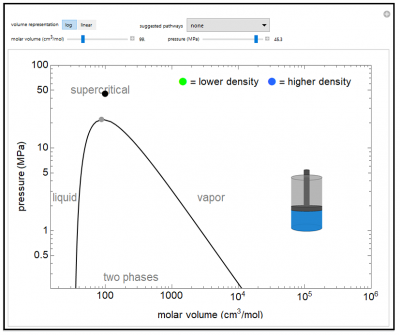
The pressure-volume phase diagram (log pressure versus log of molar volume) is shown for water. This demonstrates typical phase behavior of a single component and illustrates the concept of state functions. Drag the black dot on the P-V plot to change pressure and volume (and temperature also changes). The piston-cylinder represents the log of the volume, so that the large differences in volume between vapor and liquid can be visualized. The fluid in the cylinder is blue when liquid and green when in vapor. The intensity of the green color increases as the fluid becomes denser.
Try to answer these questions before determining the answer with the simulation. We suggest that you write down the reasons for your answers.
- If a vapor-liquid mixture is heated in a fixed volume container does it eventually become all liquid or all vapor?
- Can a liquid be converted to a vapor without a visible phase change?
In this Demonstration, liquid propane is injected into an evacuated 2-L spherical tank that is held at constant temperature. Depending on the number of moles injected and the temperature (control both with sliders), the propane either vaporizes completely or forms two phases in vapor-liquid equilibrium (VLE). When propane is in VLE, the tank pressure equals the saturation vapor pressure of propane; otherwise, the pressure is calculated using the ideal gas law. The pressure is displayed at the top of the tank. Click the play button next to “inject liquid” to inject liquid into the tank. The intensity of the blue color of the vapor is proportional to the vapor density. The volume of the liquid in the tank exaggerated relative to the vapor volume for better visualization. The bar graph to the right shows the number of moles of liquid and vapor in the tank.
Try to answer these questions before determining the answer with the simulation. We suggest that you write down the reasons for your answers.
- If 0.15 L of liquid are injected into a 2-L evacuated tank, what are the possible phases present at equilibrium?
- Suppose when 0.10 L of toluene are injected isothermally into an evacuated tank and vapor and liquid are present at equilibrium. What phases are present if an additional 0.10 L of toluene is injected?
- Suppose 1.0 mol of propane is injected into an evacuated tank and 0.03 mol of liquid propane is present at equilibrium. If 0.90 mol of propane were injected in the evacuated tank at the same temperature, approximately how many moles of liquid propane would be present?
Here is another optional simulation that shows the circumnavigation of the critical point on a pressure-temperature diagram.