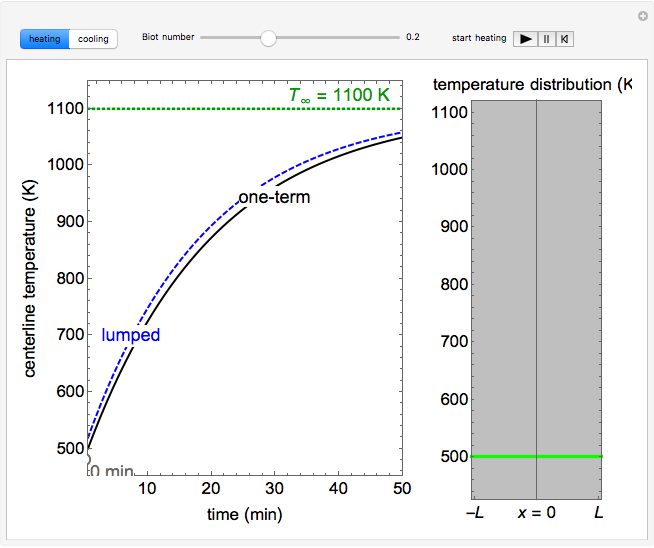
A plane wall of thickness 2L is initially at uniform temperature. At time t = 0, its surface is exposed to a liquid at a different temperature. The centerline temperature (at x = 0) is plotted as a function of time on the left, and the temperature distribution as a function of location is plotted on the right; it varies in time. Click the “start heating” or “start cooling” play button to initiate heating or cooling. For heating, the initial temperature is 300 K, and for cooling the initial temperature is 800 K. During heating, the fluid temperature is 1100 K (green line), and for cooling, the fluid temperature is 300 K. Because the exact solution to the transient heat conduction equations gives an infinite series, the first term in the series was used to calculate temperature as a function of time and location; the black line in the left plot shows the one-term solution. The dashed blue line is the lumped capacitance solution, which is nearly the same as the one-term solution at low Biot numbers, but it deviates significantly at high Biot numbers. Set the Biot number with a slider. The lumped capacitance method assumes that the plane wall temperature is uniform at a given time. The Biot number is a dimensionless ratio of convection at the surface to conduction within the solid.