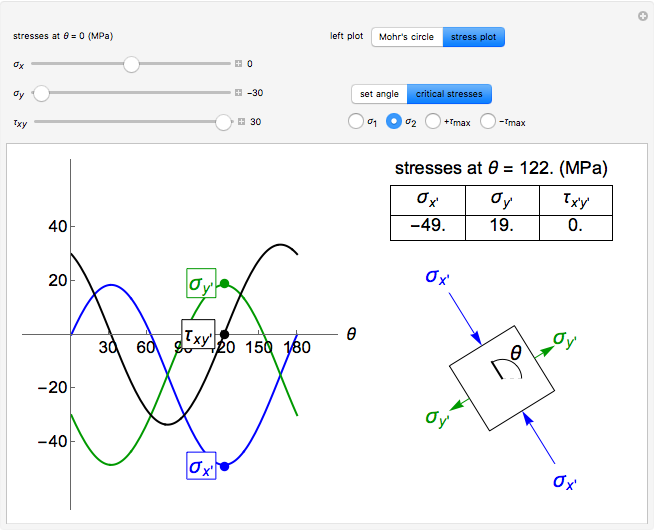
This simulation uses a Mohr’s circle and a stress plot to show the effects of stress transformation on a differential element or area. Use sliders to vary the stresses σ_x, σ_y, and τ_xy, which correspond to the stresses on the differential element at θ = 0° (dashed black line). Select “set angle” to vary the angle θ with a slider. Stress transformation equations are used to compute the transformed stresses σ_x’, σ_y’, and τ_x’y’ (solid black line), which are shown on the differential stress element as blue, green, and black arrows, respectively. Select “Mohr’s circle” button to display Mohr’s circle on the left. An angle of θ on the differential stress element corresponds to an angle of 2θ on the Mohr’s circle. Select the “stress plot” button to display a plot of all three transformed stresses versus θ on the left. Select “set angle” to set θ with a slider or “critical stresses” to snap the diagram to the angle of one of the principal stresses (σ₁ and σ₂) or one of the maximum in-plane shear stresses (+τ_max and -τ_max). Note that Mohr’s circle is displayed with positive +τ_xy in the downward direction, so an increase in θ results in a counterclockwise rotation on both the Mohr’s circle and the differential stress element.