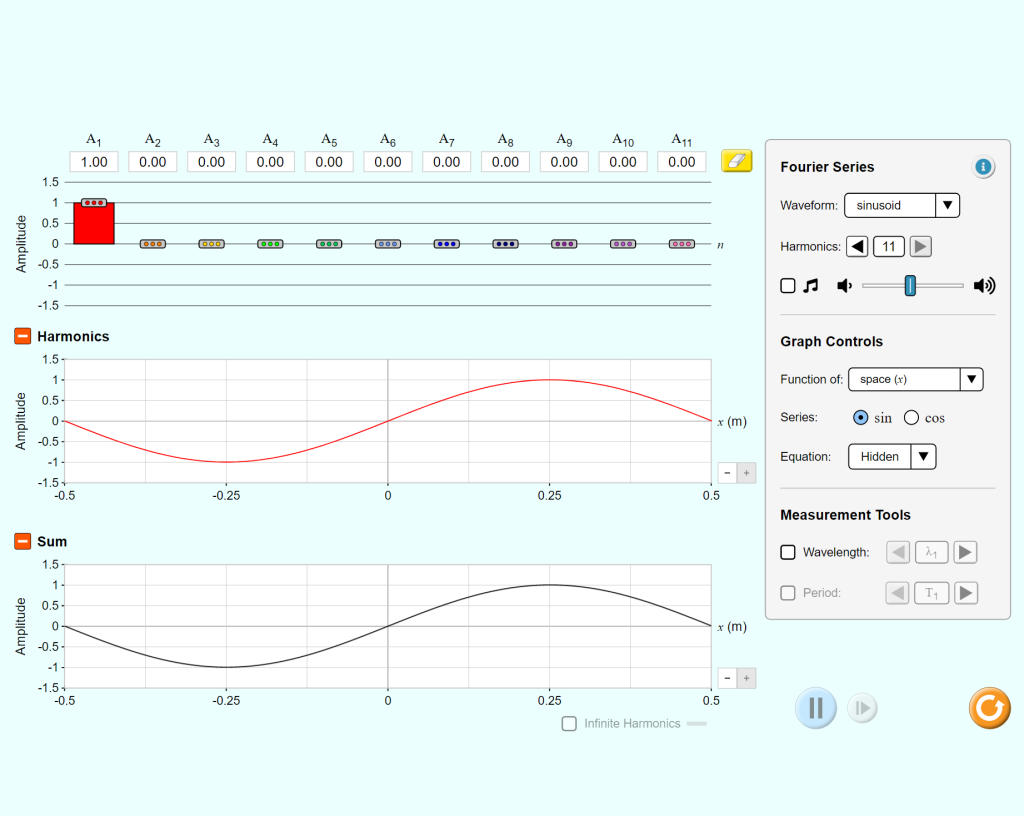
Discover qualitatively how sines and cosines add up to produce arbitrary periodic functions. A Fourier series is an expansion of a periodic function into a sum of trigonometric functions. In this simulation, you can create arbitrary waves by combining individual harmonics of different wavelength and amplitude. Included is also a “wave game” where you try to recreate a wave by constructing it from individual sinusoids.