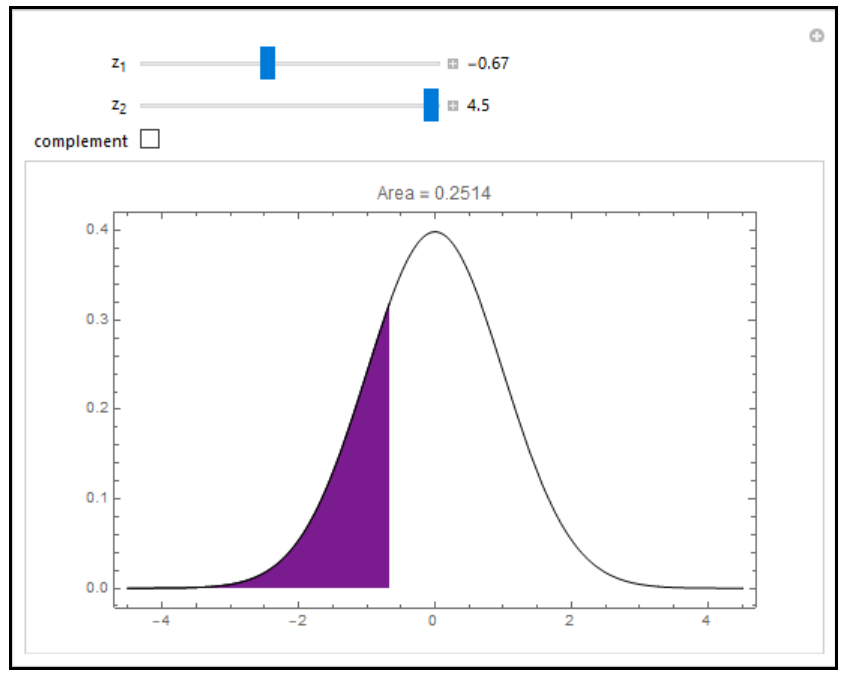
This simulation provides a dynamic supplement to elementary statistics textbooks that show how to use a table of standard normal cumulative probabilities. As you slide z₁ along, holding z₂ fixed at the upper limit, these probabilities are obtained as the area shown under the curve. Moving z₂ to the left, the upper area probability is added to the area to the left of z₁. The probability corresponding to the interval between z₁ and z₂ is obtained by taking the complement. You can see that the probability corresponding to the interval (-0.67, 0.67) is close to 0.5. This simulation also illustrates the “68-95-99.7 rule” that, in a normally distributed population, about 68% of the observations fall within one standard deviation, 95% fall within two standard deviations, and 99.7% fall within three standard deviations.