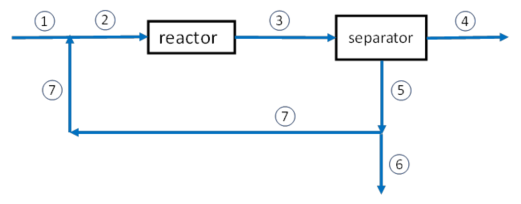
Material balances on mixing point

\(\dot{n}_2 = \dot{n}_1 + \dot{n}_7\)  (Note that this equation is not independent of the balances of the individual components below.)

\(x_{i,2}\,\dot{n}_2 = x_{i,1}\,\dot{n}_1 + x_{i,7}\,\dot{n}_7\) (one equation for each component \(i\))

where \(\dot{n}_j\) = total molar flow rate at location \(j\) (\(j\) = 1 – 7)

\(x_{i,j}\) = mole fraction of component \(i\) at location \(j\)

Material balances on reactor

For reactants only and assuming a stoichiometric feed

\(x_{i,3}\,\dot{n}_3 = x_{1,2}\,\dot{n}_2 \cdot (1\, – \, X)\) (where component 1 is a reactant; one equation for each reactant)

For products only

\(x_{i,3}\,\dot{n}_3 = x_{1,2}\,\dot{n}_2 \cdot X \cdot a\) (where component 1 is a reactant; one equation for each product)

where \(a\) is the stoichiometric coefficient of the product 

\(X\) = fractional conversion of reactants (stoichiometric feed)

For unreactive species

\(x_{i,2}\,\dot{n}_2 = x_{i,3}\,\dot{n}_3\)

Material balances on separator

(In general, a separator may not remove all of the reaction product and/or it may also remove some of the feed species.)

\(\dot{n}_3 = \dot{n}_4 + \dot{n}_5\)  (Note that this equation is not independent of the balances of the individual components below.)

\(x_{i,3}\,\dot{n}_3 = x_{i,4}\,\dot{n}_4 + x_{i,5}\,\dot{n}_5\) (one equation for each component \(i\))

Material balances on splitting point

\(\dot{n}_5 = \dot{n}_6 + \dot{n}_7\) (Note that this equation is not independent of the balances of the individual components below.)

\(\dot{n}_6 = purge \cdot \dot{n}_5\)

\(\dot{n}_7 = (1\, -\, purge) \cdot \dot{n}_5\)

\(x_{i,5} = x_{i,6} = x_{i,7}\) (one equation for each component \(i\))

where \(purge\) = the fraction of stream 5 that is purged

Overall atom balances 

(Note that these equations are not independent of the above equations.)

molar flow rate of atomic species in (stream 1) = molar flow rate of atomic species out (stream 4 + stream 6) for each atomic species in the feed