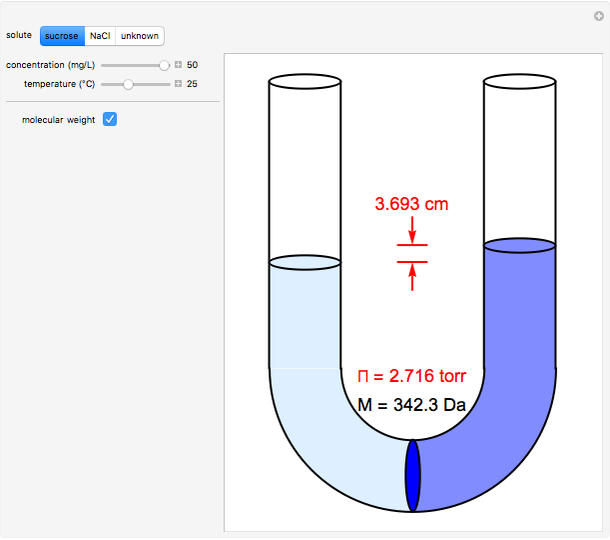
Osmosis involves the selective passage of certain components of a solution through a semipermeable membrane, with exclusion of other components. In this simulation, the membrane is permeable to water, but impermeable to the solute in a water solution. The membrane (blue disk at the bottom of the U-tube) separates the water on the left from an aqueous solution on the right. Water spontaneously flows through the membrane into the solution, in an attempt to equalize the concentrations on the two sides. This gives rise to an osmotic pressure (Π). For dilute solutions, the osmotic pressure, in atm, is well approximated by the van ‘t Hoff equation, Π = i[X]RT, where [X] is the solute concentration in mol/L, R = 0.082057 L atm/(mol K), the ideal-gas constant, and T, the absolute temperature in K. The van ‘t Hoff factor (i) represents the number of ions per molecule for a dissociated solute. For NaCl, the value of i is two. The other solutes in this simulation are undissociated. The van ‘t Hoff equation can be written in a form analogous to the ideal gas law: ΠV = n_xRT, but the underlying mechanisms for the two phenomena are completely different. Osmotic measurements provide a sensitive method for determining molecular weights M, particularly for polymers. For a solute concentration of c_x g/L, the molar concentration [X] is equal to c_x/M.