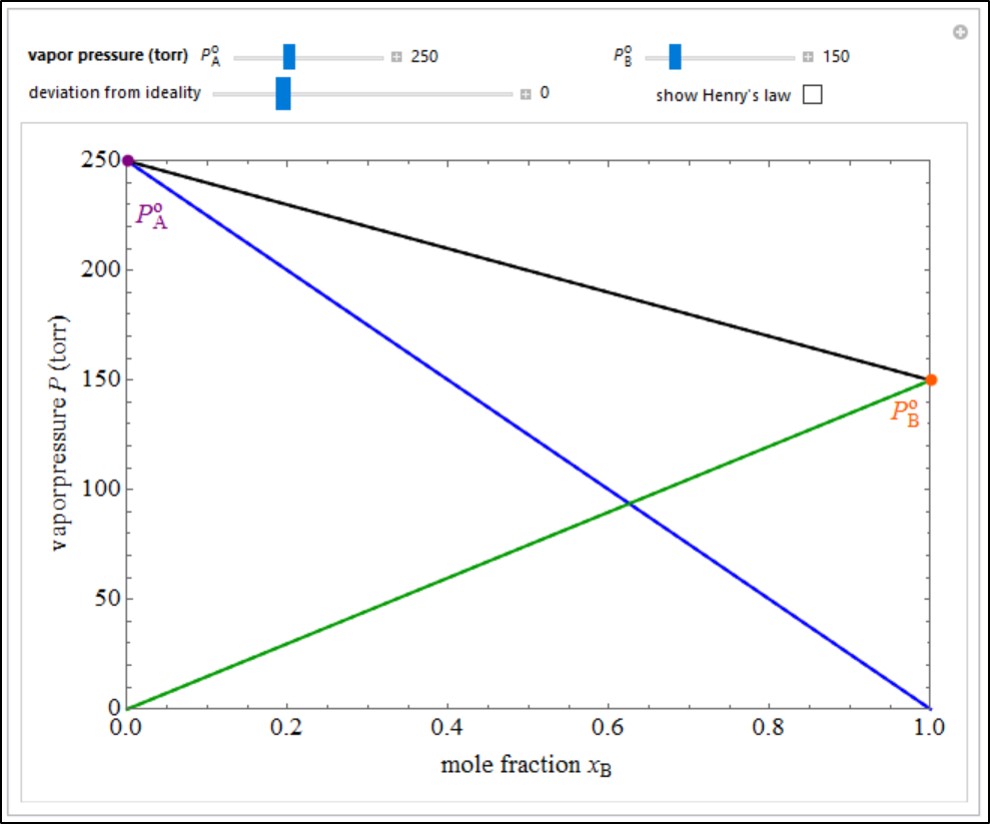
An ideal solution of two liquids A and B obeys Raoult’s law, which states that the partial pressure of each component is proportional to its mole fraction: P_A = P_A^ox_A and P_B = P_B^ox_B, where P_A^o and P_B^o are the vapor pressures of the pure components at a given temperature. The total pressure is then P= P_A + P_B = P_A^o(1 – x_B) + P_B^o. Most real solutions exhibit deviations from Raoult’s law. A positive deviation is characterized by P_A > P_A^ox_A and P_B > P_B^ox_B and indicates that the attractive interactions between like molecules is greater than that between A and B molecules. A negative deviation has P_A < P_A^ox_A and P_B < P_B^ox_B, implying stronger mutual interactions between unlike molecules. The curves shown in the graphic are qualitative approximations to the actual dependence of vapor pressures on composition. The blue and green curves represent the partial pressures of A and B, respectively, while the black curve shows the total vapor pressure. The dashed lines refer to the hypothetical ideal behavior of the corresponding vapor pressures. For nonideal solutions, Raoult’s law is asymptotically approached for x_A or x_B ≈ 1. Dilute solutions, on the other hand, are approximated by Henry’s law: the linear relations P_A ≈ K_Ax_A for x_A ≈ 0 and P_B ≈ K_Bx_B for x_B ≈ 0. Check “show Henry’s law” to show this behavior, dotted purple and orange lines represent Henry’s law. Set the vapor pressures of the liquids and the deviation from ideality with sliders. Move the mouse over a curve to see its label (real or ideal).

Download this simulation

This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.

About:

Author: S. M. Blinder, modified by Rachel Baumann and John L. Falconer. Open content licensed under CC BY-NC-SA

View the source code for this simulation